过拟合

什么是过拟合？

如下图，这三个都是房屋面积与房屋售价的关系的散点图，我们用三种模型去拟合这些点。

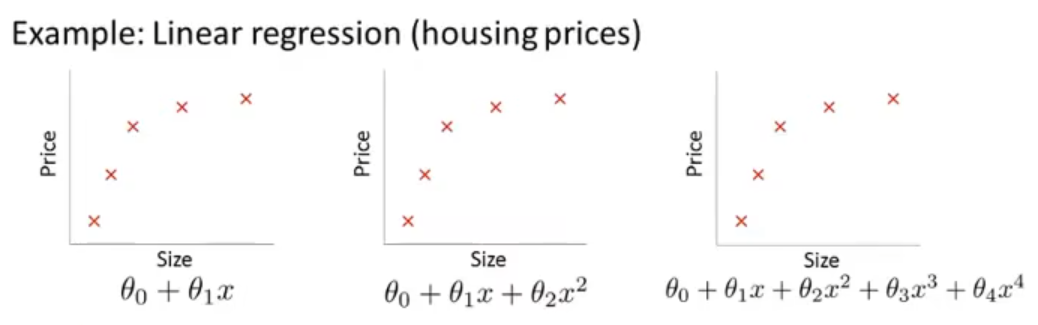
左边是直线： $\theta_0+\theta_1x$

中间是抛物线： $\theta_0+\theta_1x+\theta_2x^2$

右边是一个多项式曲线： $\theta_0+\theta_1x+\theta_2x^2+\theta_3x^3+\theta_4 x^4$

最终的拟合结果可能如下：

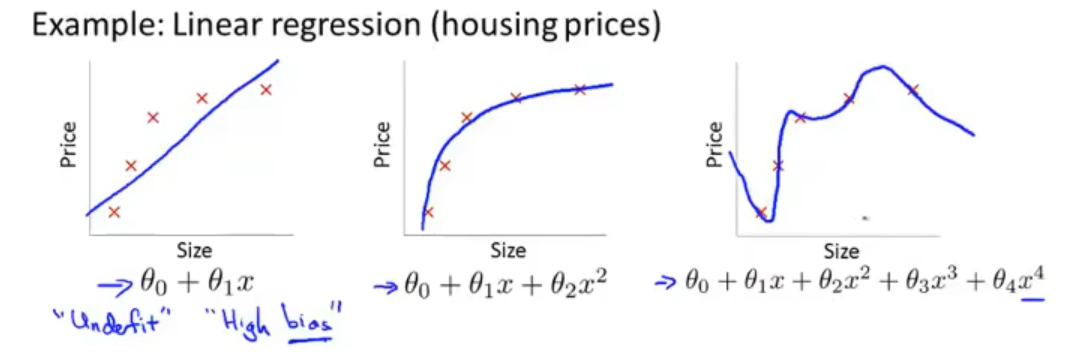
在上图中，左边是欠拟合、右边是过拟合。

欠拟合相对容易理解，就是模型过于简单使得最后的出来的结果与实际的结果偏差比较大；而过拟合看上去对训练样本的表现很好，但是对于没有出现在训练集中的样本（泛化）可能表现很差，也就是其泛化能力差。

逻辑回归的过拟合

在分类问题中，我们在确定决策边界的时候也可能会存在过拟合问题，如下图

很明显左边也是欠拟合、而右边是过拟合

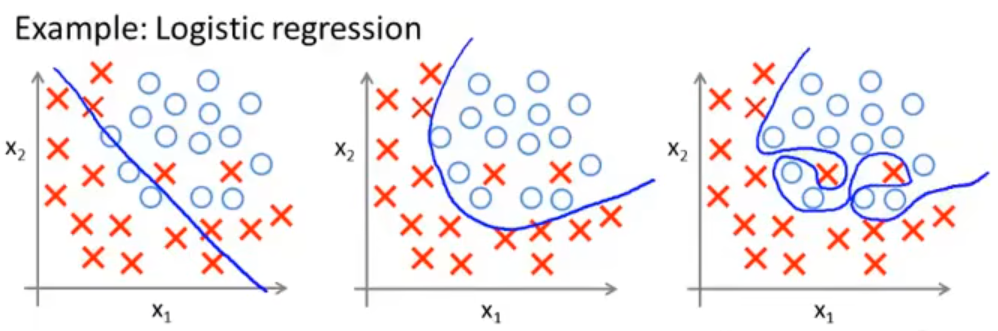
如何解决过拟合

第一种办法，减少特征变量，用那些比较重要的变量。而减少特征变量的办法又有两种：

人工选择需要保留的重要变量
使用模型选择算法选择保留的变量，当然我们在舍弃一些变量的时候，实际上也舍弃了一些可能比较重要的信息，有时候我们不能这么干。

第二种办法，正则化。保留所有的特征变量，但是通过调整特征变量前面参数来改变它的重要性，这在有很多对结果有影响的特征变量的时候可能会比较有效。

正则化

什么是正则化？

在上述过拟合的例子中，通过加入多个高阶项（ $\theta_3x^3、\theta_4x^4$ ）就会导致过拟合的现象，那么我们有没有办法在引入高阶项的时候避免过拟合的发生呢？

很显然，我们只需要将 $x^3、x^4$ 前面的系数 $\theta$ 变小就可以使该高阶项的重要性变小，从而减小过拟合。

而系数变小则是通过优化代价函数来实现，通过在代价函数（这里使用线性回归的代价函数作为示例）后面加入惩罚项（1000是随便选的一个比较大的数），使得最终的代价函数变大了，因此这时的 $\theta_3、\theta_4$ 必须比较小才行。这是我们解决引入高次项之后会造成过拟合问题的一般思路。

\min\limits_{\theta}\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+1000\ \theta_3^2+1000\ \theta_4^2

然而，现实中的问题是，我们大部分时候是不知道哪些参数是重要的影响因素、哪些是不重要的影响因素，和上面的思路类似，继续对代价函数进行改写

J(\theta)=\frac{1}{2m}[\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^n\theta_j^2]

同理，在代价函数后面加上了惩罚项，目标也是为了减少那些对最终取值影响不大的自变量的影响，其中的参数 $\lambda$ 是正则化参数。

这个新的代价函数有两项，我们在进行训练的时候，第一个目标就是更好的拟合数据，和代价函数的第一项有关；第二个目标就是保持参数尽量小，防止过拟合，和代价函数的第二项有关。而参数 $\lambda$ 能够平衡这两个目标。

通过正则化，得到的拟合曲线就会变得更加平滑和泛化：

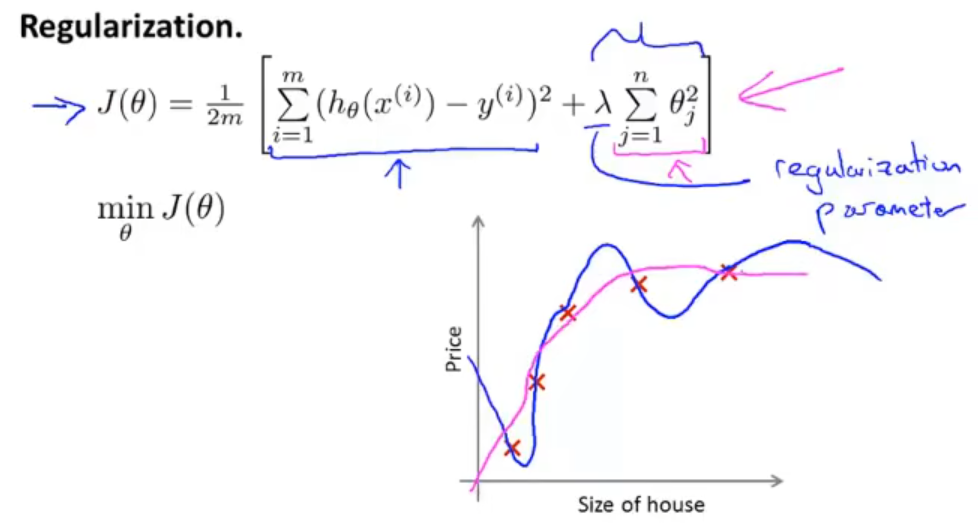
而对于参数 $\lambda$ 的选择是非常重要的，过小可能正则化效果不好，过大可能会导致所有自变量系数趋向0，最终只剩下常数项。无论哪种都得不到很好的拟合效果。

线性回归的正则化

梯度下降与正则化

梯度下降法寻找使代价函数最小的 $\theta$ ，基本算法是给定一个初始的 $\theta_0$ ，然后通过不断的迭代来优化：

\theta _{0}:=\theta _{0}-\alpha\dfrac{1}{m}\sum ^{m}_{i=1}\left( h_{\theta }\left( x^{\left( i\right) }\right) -y^{\left( i\right) }\right)x_{0 }^{(i)} \\ \theta _{j}:=\theta _{j}-\alpha\dfrac{1}{m}\sum ^{m}_{i=1}\left( h_{\theta }\left( x^{\left( i\right) }\right) -y^{\left( i\right) }\right)x_{j}^{(i)}

而在正则化算法是针对从 $\theta_1$ 开始的所有参数，因此在上述算法的基础上加上惩罚项：

\theta _{0}:=\theta _{0}-\alpha\dfrac{1}{m}\sum ^{m}_{i=1}\left( h_{\theta }\left( x^{\left( i\right) }\right) -y^{\left( i\right) }\right)x_{0 }^{(i)} \\ \theta _{j}:=\theta _{j}-\alpha[\dfrac{1}{m}\sum ^{m}_{i=1}\left( h_{\theta }\left( x^{\left( i\right) }\right) -y^{\left( i\right) }\right)x_{j}^{(i)}+\frac{\lambda}{m}\theta_j]

然后继续对该式子进行变换，得到：

\theta _{j}:=\theta _{j}(1-\alpha\frac{\lambda}{m})-\alpha\dfrac{1}{m}\sum ^{m}_{i=1}\left( h_{\theta }\left( x^{\left( i\right) }\right) -y^{\left( i\right) }\right)x_{j}^{(i)}

然后与原先的梯度下降法的式子进行对比，可以发现后半部分是一样的，而前半部分的参数 $\theta_j$ 多了 $(1-\alpha\frac{\lambda}{m})$ ， $\alpha$ 是学习率、一般很小， $m$ 是样本数、一般很大，因此这是一个只比1略小的数。在加入正则项后，进行梯度下降法寻找参数 $\theta$ 的时候就没有那么激进，在原有基础上让这个参数乘上一个比1略小一点的数，从而让它缩小一点，减少震荡。

正规方程与正则化

正规方程就是用训练样本的自变量设计一个矩阵，然后再把对应的输出构建为一个向量，最后再通过公式计算出 $\theta$

X=\begin{bmatrix} (x^{(1)})^T \\ (x^{(2)})^T \\ \ldots \\ (x^{(m)})^T \end{bmatrix}\quad\quad y=\begin{bmatrix} y^{(1)} \\ y^{(2)} \\ y^{(3)} \\ \ldots \\ y^{(m)} \end{bmatrix} \\\\ \theta=(X^{T}X)^{-1}X^{T}y

然后给这个式子加上正则项，就变成了下面这个样子

A=\begin{bmatrix} 0 \\ & 1 \\ && 1 \\ &&& \ldots \\ &&&& 1\end{bmatrix} \quad(n+1)×(n+1)\\ \theta=(X^{T}X+\lambda A)^{-1}X^{T}y

那么在加入了正则项之后，括号里的东西一定能够保证可逆么。

在之前的文章中提到，如果样本数 $m\le$ 特征数 $n$ ，那么原式子中的 $X^TX$ 是不可逆的（奇异矩阵）。

但在引入了正则项之后，如果 $\lambda>0$ ，括号中的东西就是可逆的，可以帮助我们解决这个不可逆问题。

逻辑回归的正则化

对于逻辑回归代价函数的优化，使用的是梯度下降的方法

在之前的文章中，逻辑回归同样也会出现过拟合的现象，使得决策边界非常扭曲，从而导致其没有泛化能力

首先，和线性回归一样，在原来的代价函数的基础上，加入正则项：

J(\theta)=-[\frac{1}{m}\sum_{i=1}^my^{(i)}\log(h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2

然后使用梯度下降法进行优化：

\theta _{0}:=\theta _{0}-\alpha\dfrac{1}{m}\sum ^{m}_{i=1}\left( h_{\theta }\left( x^{\left( i\right) }\right) -y^{\left( i\right) }\right)x_{0 }^{(i)} \\ \theta _{j}:=\theta _{j}-\alpha[\dfrac{1}{m}\sum ^{m}_{i=1}\left( h_{\theta }\left( x^{\left( i\right) }\right) -y^{\left( i\right) }\right)x_{j}^{(i)}+\frac{\lambda}{m}\theta_j]

可以看到和线性回归一样，只是假设函数 $h_\theta(x)$ 不同

总结

过拟合现象是一种常见现象，会使得模型的泛化能力下降，由此提出了一种常见的解决方法：正则化，而正则化就是通过在代价函数后增加一项惩罚项，用于限制参数 $\theta$ 的大小，从而使得模型图像更加的平滑、泛化能力得到增强。