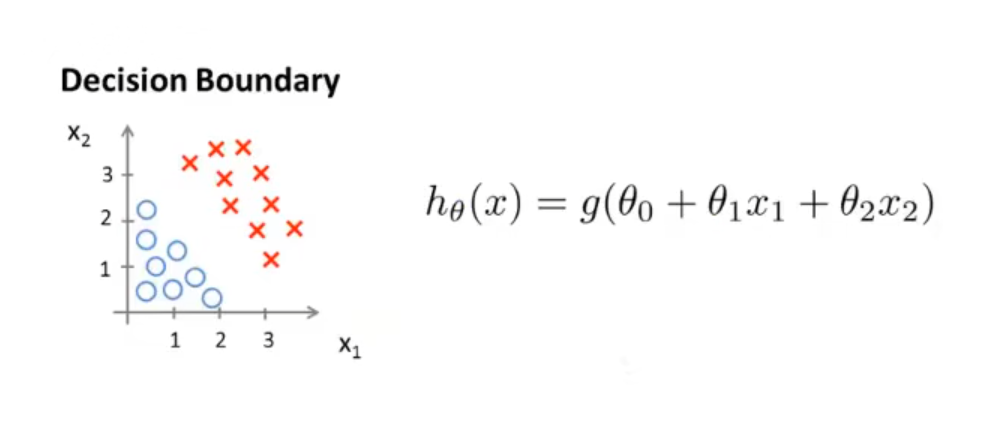逻辑回归函数
逻辑回归需要将函数的取值落在 [0,1]这个区间上,那怎么样才能让这个函数取值落在 [0,1]之间呢?
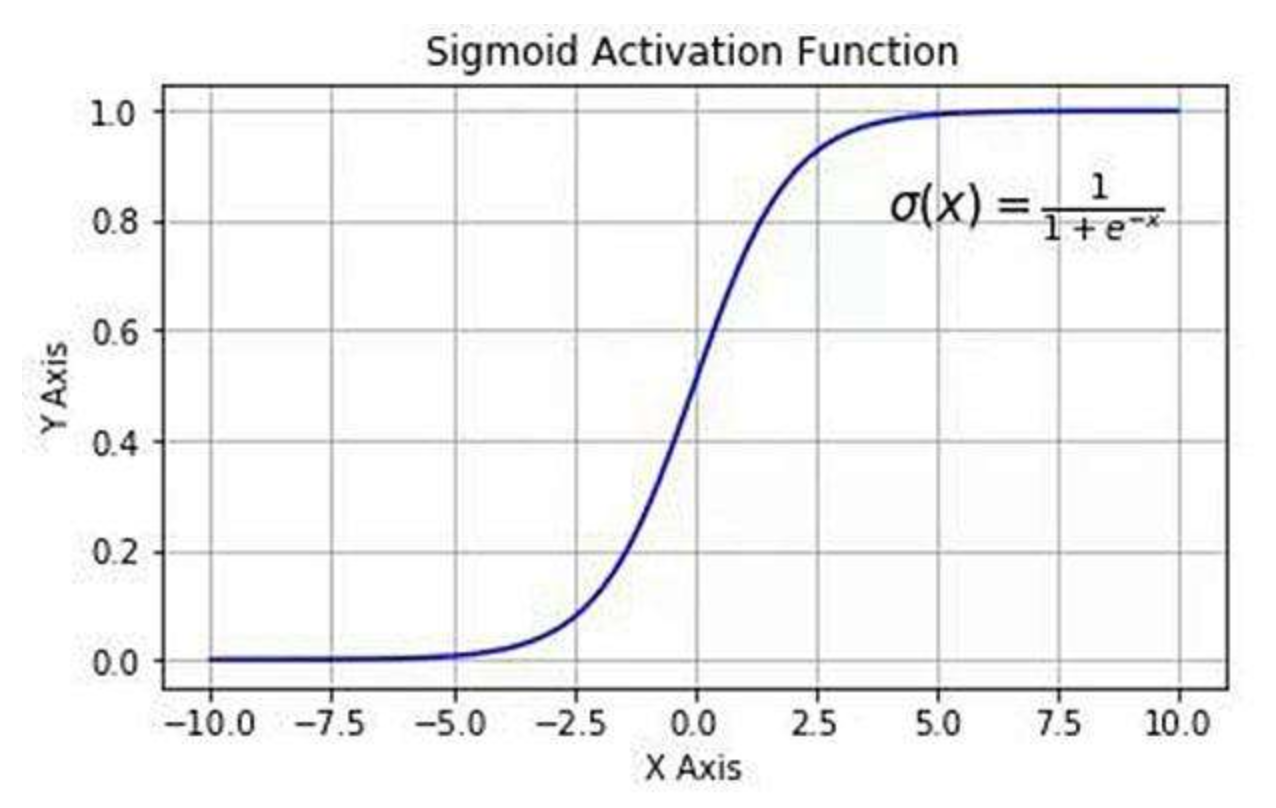
逻辑(logistic)函数其实也就是经常说的 sigmoid 函数,它的几何形状是一条S型曲线。
f(x)=1+e−x1
该函数具有如下的特性:当 x 趋近于负无穷时,y 趋近于0;当 x 趋近于正无穷时,y 趋近于1;当 x=0 时,y=0.5。
因此该函数非常适合用来作为逻辑回归模型的假设函数,原来的假设函数是:hθ(x)=θTx,通过 sigmoid 函数进行变换之后,就能得到一个新的假设函数:
hθ(x)=1+e−θTx1
优点:
- Sigmoid 函数的输出映射在(0,1)之间,单调连续,输出范围有限,优化稳定,可以用作输出层。
- 求导容易。
缺点:
- 由于其软饱和性,容易产生梯度消失,导致训练出现问题。
- 其输出并不是以0为中心的。
决策边界
在假设函数中,我们取的值一般都是一个连续的值,但我们要分类的结果 y 是离散的,不是0就是1。
因此通过以一个数值为界限,例如以0.5为界限,当 sigmoid 函数取值大于等于0.5时取1,否则取0。
线性决策边界
假设在一个二维平面上有这样一堆点,平面上的所有点是由横坐标、纵坐标两个自变量确定的。如下图:
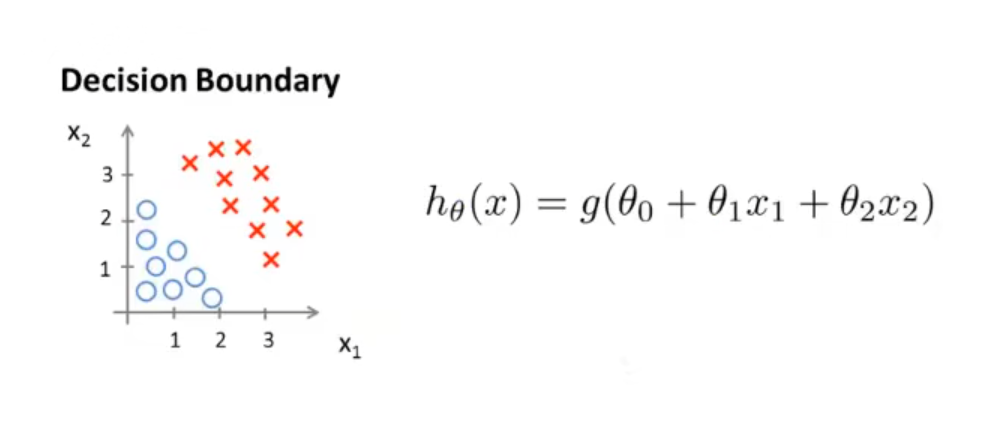
假设此时我们已经拟合好了参数 θ ,值为 ⎣⎢⎡−311⎦⎥⎤,画出该假设函数的图像,这条直线就是决策边界,分类器就是通过这个决策边界进行分类的。
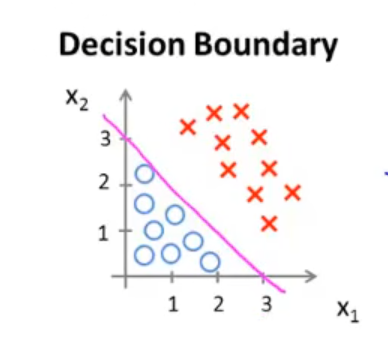
非线性决策边界
假设这些点如下图所示,很明显这不能用一条直线来作为决策边界,因此就需要更加复杂的函数来进行拟合。
如:hθ(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x22)
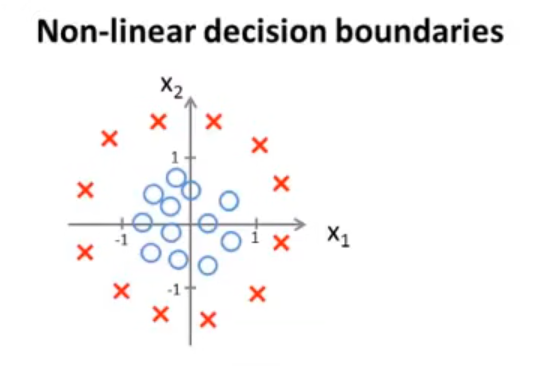
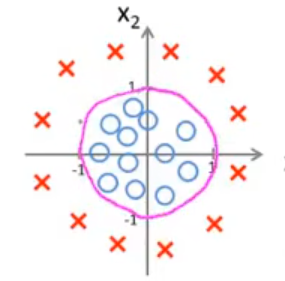
通过拟合出参数 θ=⎣⎢⎢⎢⎢⎢⎡−10011⎦⎥⎥⎥⎥⎥⎤ 后,假设函数表示的图像就变成了一个圆,这个圆也就是我们的决策边界。
总结
通过逻辑回归寻找决策边界,而决策边界由函数的形式和函数的参数共同决定。
逻辑回归中的代价函数
代价函数
我们要想找到最合适的参数,就要有一个衡量参数好坏的标准,而这个标准我们就叫做代价函数(cost function)
假设有 m 个训练样本:(x(1),y(1)),(x(2),y(2)),…,(x(m),y(m)),每个 x 都是一个向量:x∈⎣⎢⎢⎢⎡x0x1…xn⎦⎥⎥⎥⎤x0=1,对应的每一个 y :y∈{0,1};假设函数如下:
hθ(x)=1+e−θTx1
那么应该如何为这个假设函数选择合适的 θ 值呢?
之前的线性回归的代价函数为:J(θ)=m1∑i=1m21(hθ(x(i))−y(i))2,这个函数的意思是在 θ 参数下的假设函数对自变量的预测值和实际值之间的差距大小的一半,最后把 m 个差距求和,其中的 cost(hθ(x),y)=21(hθ(x(i))−y(i))2 就是第 i 个样本所花费的代价。
但是在逻辑回归中,因为假设函数是非线性的,从而导致这个代价函数不是一个凸函数,它的图像大概长这样,在使用梯度下降法求解最小值时及其容易陷入局部最优,从而导致代价函数无法轻易收敛到全局最优。
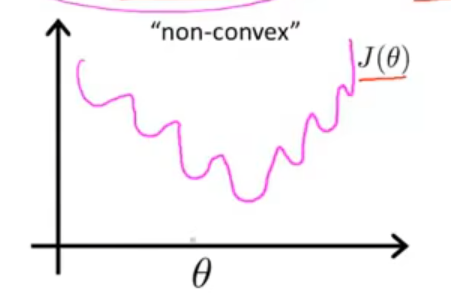
因此我们需要将这个代价 cost(hθ(x),y) 进行改写:
cost(hθ(x),y)={−log(hθ(x)), ify=1−log(1−hθ(x)),ify=0
然后将这两种情况进行合并即可得到:
cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
- 当 y=1 时,hθ(x) 越接近1,代价越小;越接近0,代价越大
- 当 y=0 时,hθ(x) 越接近1,代价越大;越接近0,代价越小
显然,这个函数明显符合我们的要求,并且该函数是一个单调函数,代入到代价函数中后得到的图像为一个凸函数,有利于梯度下降得到最小值。
参数拟合
有了上述的代价函数后,我们就可以对其中的 θ 参数进行拟合了。
J(θ)=−m1[i=1∑my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
我们可以使用梯度下降法进行拟合,求出 θminJ(θ) ,从而得到对应的参数值,和线性回归的求法一样,都是给出一个初始的参数 θ ,然后往梯度下降的方向走 α 倍的一小步,不停的进行迭代,最后找到最低点。
多分类问题
上述我们解决的都是二分类问题,而面对多分类问题,数据集看起来是这样的:
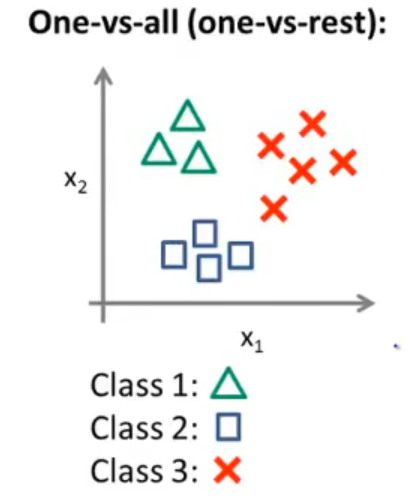
对于上述多分类问题,我们要将其转换为3个独立的二分类问题,也称为“一对余”方法,这样就将这个三分类问题转换成了3个标准的逻辑回归二分类问题。
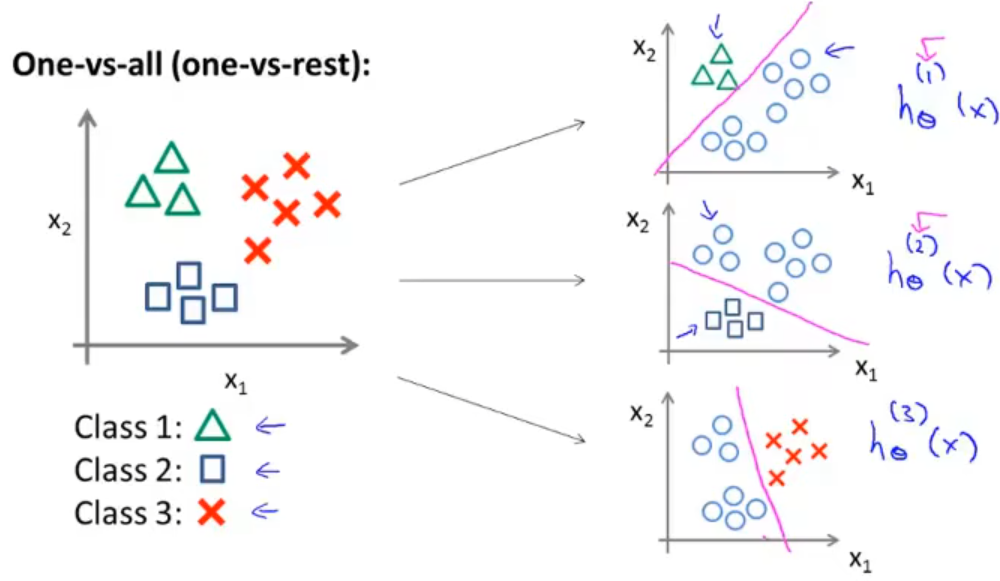
最后我们就拟合了3个假设函数作为分类器:
hθi(x)=P(y=i∣x;θ)(i=1,2,3)
然后在给定 x 后,得到的是属于第 i 个分类的概率,这个时候只需要选择可信度最大的作为 x 所属的分类即可,也就是求 imaxhθi(x)。