代价函数与梯度下降
代价函数公式示例:J(θ0,θ1)=2m1∑i=1m(hθ(x(i))−y(i))2
h函数表示假设函数,示例(线性函数):hθ(x)=θ0+θ1x
梯度下降公式示例:θj:=θj−α∂θj∂J(θ0,θ1)(forj=0andj=1)
将代价函数代入偏导即可得到:θj:=θj−αm1∑i=1m(hθ(x(i))−y(i))xj(i)
α表示学习率
学习率越大则梯度下降的速度越快,但容易错过代价值最小的位置;
α后面跟着的是点(θ0,θ1)的梯度,用来确定代价函数的最小值的位置
更新梯度时需要 同步更新:
- temp0:=θ0−α∂θ0∂J(θ0,θ1)
- temp1:=θ1−α∂θ1∂J(θ0,θ1)
- θ0:=temp0
- θ1:=temp1
错误做法:
- temp0:=θ0−α∂θ0∂J(θ0,θ1)
- θ0:=temp0
- temp1:=θ1−α∂θ1∂J(θ0,θ1)
- θ1:=temp1
多元梯度下降
(多元线性回归)假设函数表示为:hθ(x)=θ0+θ1x1+θ2x2+…+θnxn=θTX
代价函数表示为:J(θ0,θ1,…,θn)=J(θ)=2m1∑i=1m(hθ(x(i))−y(i))2
梯度下降公式表示为:θj:=θj−α∂θj∂J(θ)
代入代价函数求偏导:θj:=θj−αm1∑i=1m(hθ(x(i))−y(i))xj(i)
特征缩放
通过确保所有特征都处在一个相近的范围,即确保不同特征的取值在相近的范围内,这样梯度下降法就能够更快地收敛
例如:
变量x1的取值范围为0-2000;变量x2的取值范围为0-5
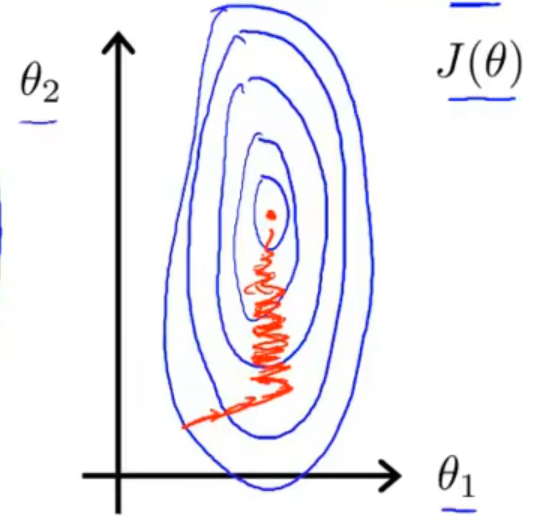
若不经过处理,这两个变量表示出来的代价函数如下图1,收敛速度比较慢。
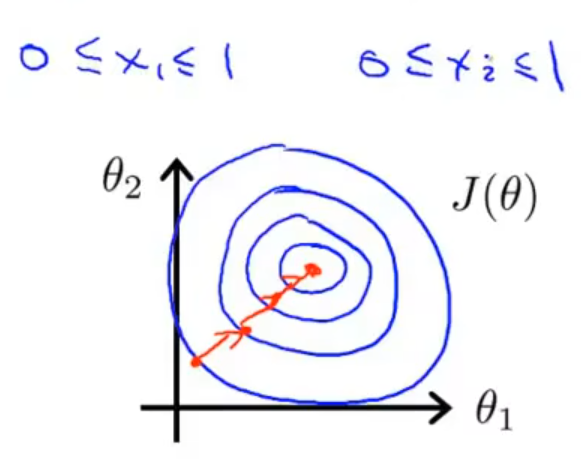
通过将这两个变量归一化,其取值都在 0-1 之间,表示出来的代价函数如下图2,收敛速度就会比较快
均值归一化:xi=sxi−μ(μ为均值,s为特征值的范围)






